Приближенное дифференциальное уравнение изогнутой оси балки, лежащей на сплошном упругом основании, имеет вид
, (1.2)
где E–модуль упругости материала балки (для рельсовой стали E = 2,1∙105МПа);
Iz – момент инерции поперечного сечения балки (рельса) относительно центральной оси /1, таблица Б1/(Iz = 3208∙10-8);
U – модуль упругости подрельсового основания, МПа (для кривой в летних условияхU=126МПа);
Введением коэффициента относительной жесткости, м-1,
(1.3)
м–1
линейное дифференциальное уравнение 4-го порядка (1.1) приводится к каноническому виду, в результате решения которого получаются следующие зависимости для прогиба y, изгибающего моментаMzи давления рельса на шпалу
Qy: 
; (1.4)
(1.5)
(1.6)
На рисунке 1.1 приведены линии влияния прогибов и изгибающих моментов пропорциональных значениям функции η(k∙x) и μ(k∙) соответственно и построенных для случая, когда 
и 
равны единице.
В случае действия на рельс системы подвижных сосредоточенных сил суммарный эффект определяется как
; (1.6)
; (1.7)
, (1.8)
где 
и 
– суммарные или эквивалентные нагрузки для опрдения изгибающего момента, прогиба и давления на шпалу для заданной системы подвижных сосредоточенных сил.
а)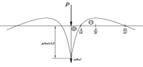 
б)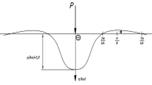
Рисунок 1.1 – Линии влияния: а – изгибабщего момента; б – упругих просадок рельса