Рi = pi δmLnBkHxTy,
в которой степени могут быть целыми или дробными, положительными или отрицательными.
Частная производная Рi по коэффициенту полноты
![]() .
.
Величину этой частной производной можно вычислить по прототипу. Частная производная функции F определяется как сумма частных производных отдельных разделов.
![]() .
.
Очевидно, что частные производные по другим переменным будут определяться подобным же образом.
Поскольку в полученном уравнении фигурируют пять неизвестных, то для решения уравнения необходимо задаться дополнительными зависимостями, для выражения одного элемента через другой. Это могут быть либо уравнения теории корабля, либо ограничения размерений, либо соотношение размерений прототипа. Последний способ выражения главных размерений является наиболее употребительным. В этом случае
![]() ,
,
откуда
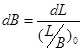 .
.
Аналогично выражаются и прочие приращения главных размерений. Коэффициент общей полноты задают исходя из статистических зависимостей, или принимают по прототипу. В первом случае dδ = δ – δ0, во втором dδ = 0.
Дифференциальное уравнение масс Бубнова
От обобщенного дифференциального уравнения масс уравнение Бубнова отличается тем, что второе слагаемое левой части [dF]0 = 0. Для учета изменения скорости хода, дальности плавания, измерителей и прочих независимых переменных И.Г.Бубнов предложил пересчитывать элементы проектируемого судна не относительно элементов прототипа, а относительно элементов какого-то судна, имеющего главные размерения и коэффициенты полноты прототипа, но независимые переменные, соответствующие проектируемому судну. Поскольку такое сочетание у реально существующих судов найти практически невозможно, необходимо изменить нагрузку прототипа, таким образом, чтобы оказались выполненными элементы технического задания проекта. Поскольку после введения изменений нагрузка прототипа не будет соответствовать водоизмещению прототипа, его необходимо компенсировать за счет независимых масс.
Общая формула определения масс разделов исправленного прототипа
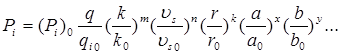 .
.
Изменение масс независимых разделов осуществляется прямым расчетом. Для компенсации получившегося расхождения между нагрузкой и водоизмещением необходимо изменить массу перевозимого прототипом груза.
