Для вывода уравнения будем рассматривать приращение высоты борта как заданную величину. Преобразуем исходное уравнение dP = dD – d(ΣPi) к виду
,
где 
– полный дифференциал переменных масс по главным размерениям подводной части и коэффициенту полноты. Объедением приращение независимых масс и приращение масс разделов вызванное изменением независимых переменных.
.
Тогда обобщенное дифференциальное уравнение можно записать в виде
.
Если вести обозначение
,
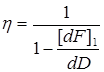где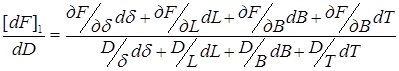 
, то обобщенное уравнение можно записать, относительно неизвестного dD, в виде
dD = ηΔ.
Зная численное значение коэффициента η можно определить приращение водоизмещения, соответствующее заданному приращению масс Δ. Но для этого необходимо исключить из уравнения неизвестные приращения элементов. Предположим, что заданное приращение Δ компенсируется за счет приращение только какого-то одного элемента. Пусть dL = dB = dT = 0, dδ ≠ 0.
Тогда
.
Можно составить такие же выражения применительно к другим элементам судна. Аналогично формуле для обобщенного коэффициента запишем формулы для частных случаев
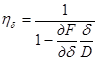для dL = dB = dT = 0, dδ ≠ 0.
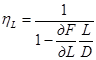для dδ = dB = dT = 0, dL ≠ 0.
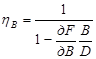для dδ = dL = dT = 0, dB ≠ 0.
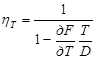для dδ = dL = dB = 0, dT ≠ 0.
Полученные коэффициенты ηδ, ηL, ηB, ηT могут рассматриваться как частные коэффициенты приращения водоизмещения по соответствующим элементам. Для определения приращения водоизмещения в каждом из случаев, по аналогии с общей формулой, можно записать
,
,
,
.
Частные коэффициенты приращения водоизмещения могут быть вычислены для каждого конкретного судна, если известны его элементы и нагрузка.
С точки зрения экономии масс выгоднее всего увеличивать водоизмещение проектируемого судна за счет тех элементов, которым соответствуют минимальным значениям коэффициентов ηi. Минимальное водоизмещение будет у того судна, у которого ηδ = ηL = ηB = ηT. Однако, это практически неосуществимо, поскольку кроме соотношения нагрузок по отдельным разделам, приходится учитывать требования к остойчивости, ходкости, вместимости и пр. Поэтому приходиться говорить не о минимальном, а о минимально возможном водоизмещении судна.
Независимое приращение масс Δ – есть сумма частных приращений.
Δ = Δδ + ΔL + ΔB + ΔT.
Разделив полученное выражение на D, получим, после подстановки значений Δi, следующую формулу
.
Из выражения dD = ηΔ получим формулу для определения η.
.
Или
.
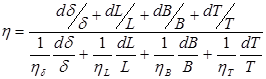Пользуясь этой формулой, легко определить значение коэффициента η для любых частных случаев.
Дифференциальное уравнение масс Нормана
Если алгебраическое уравнение масс, выраженное в функции водоизмещения привести к виду
Р = D – ΣPi(D, υs, r, a, b,…),
в котором, как и раньше а, b – какие-то независимые переменные, то при дифференцировании, с учетом выведенных ранее формул, получим